Introduction

Hydrogen molecule which is now attracting attention as energy source of fuel cell, has two different nuclear spin isomers such as ortho hydrogen (the same direction pair) and para hydrogen (the opposite direction pair). Both ortho and para hydrogen show the same chemical property, while their physical property such as specific heat is different from each other, and since the conversion between ortho and para needs extremely long time, each molecule tends to be handled as different from the other. The abundance ratio of ortho-para in hydrogen gas in ambient temperature is stable as approx. 3: 1, but when it is cooled to liquid state, most hydrogen molecule becomes para hydrogen. However a part of ortho hydrogen also becomes to liquid state, and ortho-para conversion in liquid hydrogen after long time may generate heat, which may affect to storage efficiency. Therefore when hydrogen gas is liquefied industrially, ortho-para conversion catalyst is necessary. In this experiment, we will describe, as an example, simple evaluation of ortho-para abundance ratio by using Raman spectroscopy which is one of the vibrational spectroscopy methods.

Experimental

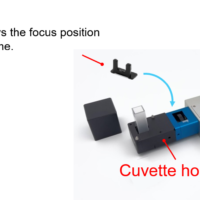
Laser Raman spectrophotometer NRS-5500 with long working distance objective lens , and 10 cm gas cell is mounted as shown in Figure 1. This long working distance function of objective lens is to focus the beam inside of the cell.

(Excitation wavelength; 532 nm, Laser power at sample point; approx. 10 mW).

Figure 1.  NRS-5500 and gas cell

Results

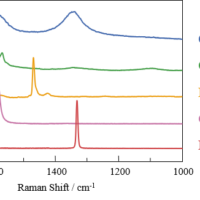
Figure 2 shows the obtained Raman spectrum of hydrogen gas. The peaks due to rotational transition were seen in the spectrum in the range from 350 to 1100 cm-1. The system temperature was estimated from Stokes anti-Stokes ratio using equation (1) to be as approx. 300K.

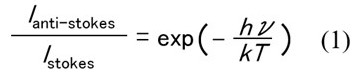
Ortho-para abundance ratio is calculated from each partition function equation (2) of ortho and para hydrogen by adding the peak height of ortho and para hydrogen in the rotation spectrum and supposing T = 300K in the equation (2), and then the ratio, approx. 7:3 was obtained. The hydrogen molecular rotation constant B in equation (2) was referred to B’=. 59 cm-1 which was calculated from the equal distance of rotation line 4B.

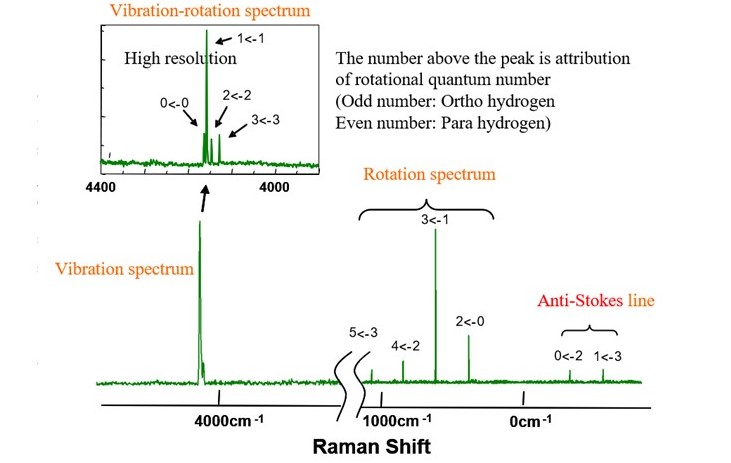
Figure 2.   Raman spectrum of hydrogen gas

 Compared to the standard ortho-para ratio of hydrogen in the ambient temperature, 3:1, the ratio of para hydrogen was higher. From this result, it can be recognized that ortho hydrogen was already converted to para hydrogen when hydrogen in the cylinder was liquefued and filled. This time, ortho-para ratio was obtained from the rotation spectrum, but when the rotation spectrum in the wavenumber region in the vicinity of peaks of rotation spectrum is affected from unnecessary light such as fluorescence generated from window, the abundance ratio can be calculated from vibration-rotation spectrum (which is) separated from the change of rotation energy by high resolution measurement of the vibration spectrum region around 4160 cm-1.

Conclusion

The reason why the difference of the direction of nuclear spin such as ortho and para hydrogen is evaluated by Raman spectroscopy (vibration spectroscopy), can be explained by quantum-mechanics. The wave function of whole hydrogen molecule can be expressed as the product of each wave function of electron, vibration, rotation and nuclear spin as shown in the equation (3).

Equation (4) and (5) show the energy of molecular vibration and rotation respectively calculated from the characteristic value  of Schrodinger equation.

Vibration energy  E = ( v + 1/2 ) hn v =0.1.2… (4)
Note, n = (1/2p)(k /m)1/2. (v: vibrational quantum number, k: force constant, m: reduced mass)

Rotation energy  E = BJ ( J + 1 ) B = h / (8p2Ic) J = 0.1.2… (5)
(B: rotational constant, J: rotational quantum number, I: inertia moment, for diatomic molecule, I =mR 2 (µ: reduced mass, R: distance between nucleus)

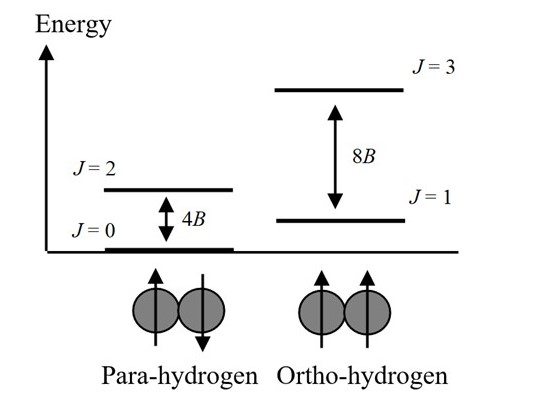
Figure 3.  Energy level of ortho-para hydrogen

 Figure 3 shows the energy level of hydrogen molecule using quantum number of rotation J. Generally in electronic ground state, wave function of electron and vibration is symmetric to the displacement of nucleus. On the other hand, wave function of nuclear spin has both symmetric and asymmetric cases to the displacement, and the each case is called as ortho and para. Wave function of rotation must be symmetric in order to satisfy the Pauli exclusion principle. Therefore ortho hydrogen exists only when rotation level J is odd (asymmetric), and para hydrogen exists only when rotation level J is even (symmetric). Nuclear spin information such as ortho and para hydrogen can be obtained from rotation spectrum (or vibration rotation spectrum) of hydrogen molecule. However, in case of Deuterium molecule (D2), Deuterium atom is Bose particle, so that the relationship between odd – even and ortho – para is contrary to hydrogen molecular case, resulting interesting phenomenon that the shape of rotation spectrum changes drastically.